Why is nature so fast?

I have lately been thinking about a rather interesting conundrum. I'm not even sure what it means to wonder about such a problem but the question is, 'why is nature so fast and our simulation of it so slow'? This statement is a rather general statement because it has the word simulation in it. There are various different ways in which natural phenomenon can be simulated so one has to be more specific here. A very simple example would be billiard balls on a table. If there are two balls on the table and the edges of the table are so far apart that we do not have to worry about the balls reflecting off of them, it's a rather simple problem to solve. One strike, one simple equation of momentum conservation and we can easily track both the balls ad-infinitum. The problem becomes exponentially more difficult when the number of balls is increased and when reflections from the edges are permitted. If the difficulty of solving a problem with 2 balls is x, the difficulty of solving a problem of 4 balls is more than 2x. And yet, the actual physical phenomenon of balls hitting each other doesn't take any more time to occur as the number of balls is increased. Another example would be the movement of stars under their mutual gravitational fields. If there are only two stars one can find an exact solution to the problem. No such solution exists even for 3 stars. In fact the time complexity for solving this problem (to arbitrary accuracy) increases as 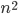where n is the number of stars considered. And yet, the stars just seem to move, completely oblivious of our own difficulties following their movements. A closer problem to my own expertise is one of mechanical and dynamical simulations but the essential idea is the same. Nature appears fast whereas our simulation of it grows exponentially slow. And I think that  it is a nontrivial question to wonder why that is the case. Is it possible to do any better? The examples I mentioned are all the more compelling because at the level of abstraction that I am talking about, we pretty much know the laws which govern the natural processes. It's not like the problem of vision where machine vision appears much more computationally intensive and slow than human vision. I think that in the vision problem we are not very sure of the underlying laws so the two problems, nature and computation, are not analogous in the sense that some physical problems are.

It appears immediately that in a natural phenomenon small parts respond simply to the stimuli provided from their nearest neighbors. A single star in a gravitational system doesn't respond immediately to the change in position of a faraway star. The gravitational information propagates at a certain speed so that it is natural that the response of a star at a certain moment is only due to its immediate neighborhood and I think this is the key problem in our current picture. We are mostly trying to solve steady state problems where the information from all parts of our domain has already reached all other parts. By steady state I just mean that we are trying to solve problems at a time scale which is much larger than the speed of information travel. This essentially means that our solution has to take into account the whole domain of the problem. In technical terms it means that we have to invert huge matrices which is a computationally intensive process with a time complexity necessarily larger than 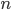. Can we do better with a paradigm shift in how we simulate the world? I cannot help but wonder.