Nonlinear guided waves
When a wave is generated in a linear material at a frequency ω, the same frequency is obtained at reception. If the material is nonlinear, we get higher harmonics in reception (2ω, 3ω...). For details, see the pdf of my paper. Lamb waves are plate waves and have two basic modes, symmetric and antisymmetric. A symmetric mode has a deformation pattern that is symmetric about the center of the plate. It was noted that in nonlinear media, the double harmonic only supported symmetric modes. It is a surprising observation because it is always difficult to excite and sustain a symmetric mode. This phenomenon was first mathematically proven by Dr. Deng in the late 90s but his approach was too complicated for application to higher harmonics. Simply speaking, the behavior of Lamb waves at the double harmonic was both experimentally known and mathematically proven. There was no knowledge, however, about how Lamb waves behave at higher harmonics. We were able to prove the following:
- Even harmonics (2ω, 4ω...) support only symmetric modes.
- Odd harmonics (ω, 3ω...) support both symmetric and antisymmetric modes.
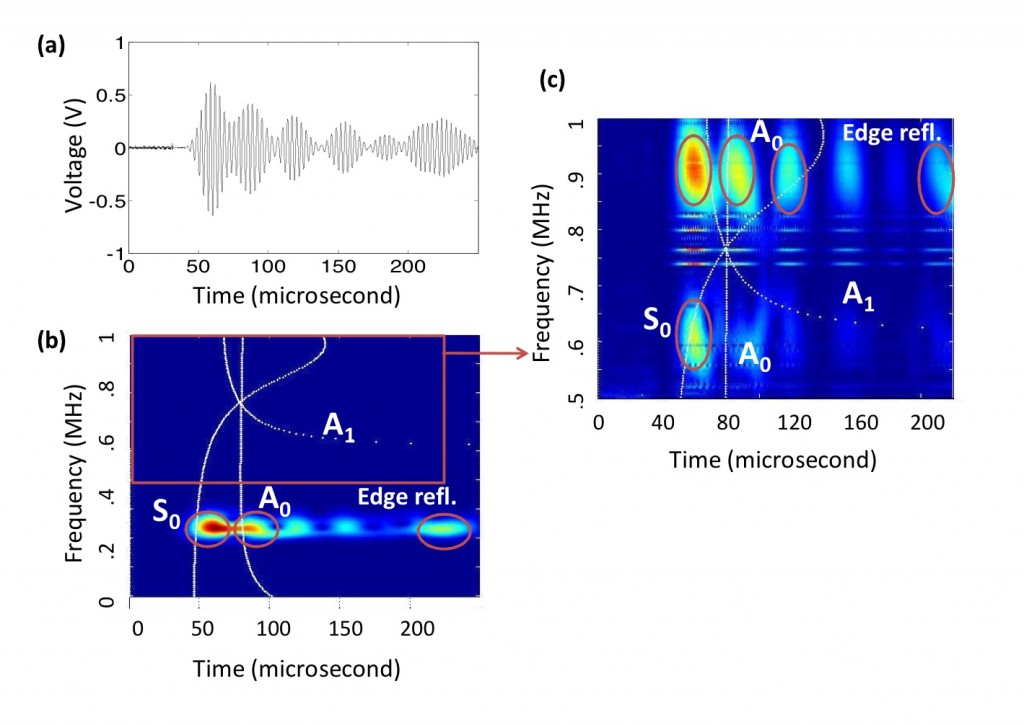
Figure below shows the experimental confirmation of the phenomenon:
The primary generation frequency was 320 kHz. We can see that both symmetric (So) and antisymmetric (Ao) modes are generated at 320 kHz (b). When we zoom into the higher frequency region, we find that at 640 kHz only the symmteric mode exists whereas all modes exist at the third harmonic (960 kHz) which confirms our predictions.
We were able to extend this reasoning to rod waves. Although mathematical predictions could be made, these were specific and complicated enough to discard any possibility of experimental verification.