Category Archive: Miscellaneous

All Greek and Latin

Posted by Ankit On July 9th, 2011

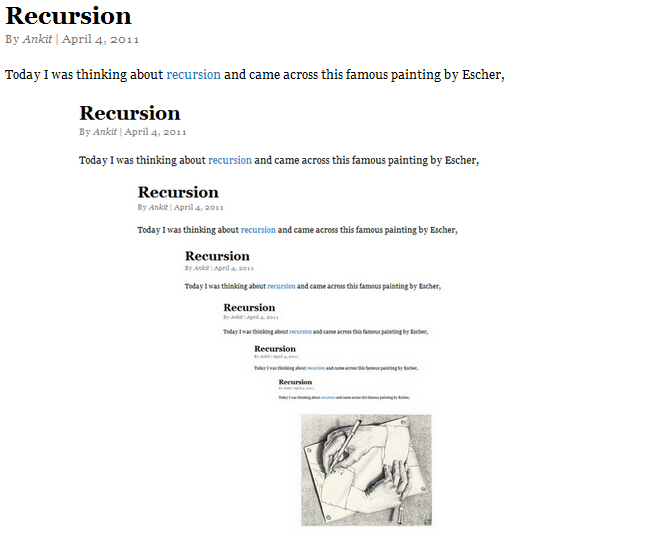
The other day I was talking to a Greek friend of mine when I realized, perhaps for the first time in my life, that there exist people in this world who actually use symbols like , 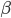etc. to communicate! I was so completely overwhelmed by this realization that I ended up spending the next half an hour imagining the various trials and tribulations that such a race must have to go through. It appeared to me, following almost as a corollary (!), that these people must be good at mathematics. That the sweet and elusive harmony of algebra which is buried somewhere deep within the machinations of the Greek alphabet must be transparent to them. By extension, obviously, these people must have a headstart in every other field which has chosen to express some subspace of this real world in this alphabet. This must evidently lead to unrealistic expectations from the young ones and it must invariably happen that every so often when a Greek is born whose genes may have mutated to not be automatically receptive to the Greek alphabet, thus leading to his subpar performance in mathematics, he must end up leading a socially isolated existence for the rest of his life. It would be a bit like being born an Indian and not being able to tolerate spice, or being born an optimistic Russian, or perhaps being born a centipede but with 99 legs. Even if we are ready to gloss over balance, such a centipede, I imagine, would try to fit in a society made up of centipedes but would be immediately frowned upon once the other centipedes count his legs. In much the same way, a Greek with subpar mathematics skills would find it difficult to justify his existence if he doesn't understand the 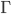function.

Then I started thinking about how the Greek alphabet is used by non-Greeks to express mathematics. It seemed to me that there exists an automatic and unsaid hierarchy of mathematical symbols in academia and one is expected to catch on to it without ever being explicitly told. People in academia tend to use Roman letters (a, b etc.) only to represent trivial things. Roman letters are likely to be used in a construction like, 'if a+b is 2 and a is 1 then what is b.' Such a construction is obviously primitive and no self respecting academician would ever accept to knowing the answer! The only people who still think seriously about such constructions are number theorists and that's only because they make the problem a tad more respectable by bringing in 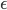in the mix. Now I do this too. I do tend to use the lower case Roman alphabet for the most trivial of things - well mostly explanatory text. Then come the capitalized Roman letters which, on their day, may be used for vectors. But when it comes to higher order tensors it's got to be Greek alphabets. Lower case Greek alphabets for the garden variety 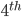order tensors but upper case ones for the most hardcore of equations which, as a corollary, must always be taken with a grain of salt.

Sometimes I wonder what the human society would have done without the invention of these symbols. This alphabet which is the mathematical equivalent of 'Here, now take me seriously,' has had a constant presence in most if not all serious scientific papers in the fields of maths, physics and engineering. I wonder how the Greeks actually deal with this problem. I asked this to my Greek friend and she thought for a bit and replied 'we use the Greek symbols for all the trivial stuff and the Roman numerals for some of the serious things.' 'Do they also walk on their heads?' I thought. I was completely stunned at this final revelation and was left reeling at the thought of reading one their papers. It would be a bit like the story of the boy who cried wolf. There was a boy who mischievously cried 'wolf' one too many times for others to believe him on the one time when he cried honestly. And there may very well be a Greek who mischievously said things were important one too many times for me to believe him on the one time when things actually may have been important.

Taos, Santa Fe, NM

Posted by Ankit On June 4th, 2011

I have been in Santa Fe, New Mexico for the whole last week to attend the 'Phononics and Metamaterials 2011' conference. Professor Nemat-Nasser was giving the principal lecture of the conference and he asked Ali and me to attend it in order to learn what the other groups have been up to. It has been a fascinating experience to listen to some of the mostÂ ingeniousÂ minds in the field and to see how much they have been able to achieve on the experimental fronts of the field of acoustic metamaterials. I realized, for the first time here, that interesting physics like negative refraction can be achieved by at least two independent paths. While our group has been working on achieving that by the use of doubly negative materials (negative density and compliance tensors), several other groups have made substantial progress by following the route of Bragg diffraction. It remains to be seen if there are advantages to following one over the other and I'm excited about the possibilities which seem to be in the offing in the next few months. Since we have the essential theoretical understanding, I expect experimental demonstrations of the doubly negative materials soon by our group.

It's not that I have been spending all my time here just going to technical talks, although doing that and thinking about the talks has occupied a much larger percentage of my time than it ever used to be the case. During the last week, I also had wide ranging discussions with Ali and came to the conclusion that he knows more about everything under the Sun than I'll ever be able to know and that he has the extremely rare talent of combining his encyclopedic knowledge with an acutely analytical mind.

I also came across a lot of interesting characters who seem to inhabit this world, which I have come to associate with a certain logic, with a rationale completely at odds with mine. But I like to listen to them with genuine curiosity, trying to find in the scales and notes of their lives, the missing song which is my own world view. I try to find in the colors of their palette, the antithesis of my own colorless (largely logical) existence. I am absolutely fascinated by the stories and experiences of such people and the cities of Santa Fe and Taos seem to throw them up with more regularity than any other place that I have visited. It's not that I necessarily want their lives for my own, but I appreciate that they have interesting stories to recount and that they lack the skepticism to believe in a fantastic, beautiful, and imaginative reality. I can listen to such people in rapt attention for hours whereas I almost instantly shut down whenever someone starts teaching me how to invest my money and hedge my bets so that I can have a comfortable retirement. Therefore, I am thankful for all those individuals who made this little trip interesting. While I don't necessarily agree with them, I am very appreciative of the fact that they exist and make life more colorful and more non-utilitarian. There was Ryan, the barista of the Santa Fe cafe 'Father sky and Mother Earth' who narrated to me his journey across the US, his experiences with meditation and the mystical traditions of the native Indian people of New Mexico, and his belief in the apocalypse of 2012. Then there was Bobby, the guitarist of the band HN88 who gifted me a CD consisting of a collection of his songs. Marianne was the barista of the great 'World Cup' cafe in Taos and told me about her transition from DC to SF to Taos and I ended up adding to the cafe's collection of foreign currencies by donating a 100 rupee note. There was a German (I forget the name) who has spent the last 20 years of his life in the little town of Taos and described himself as a starving artist. He was trying to convey to me his vision of the world as a conceptual artist but I guess my brain has ossified under the influence of logic to an extent where it's not flexible enough to appreciate orthogonal logic. Annamelia was the singer and Matt was the forest officer and finally Johnny was the ex-physicist from Los Alamos who has been collecting obscure memorabilia relating to the automobile and the transportation industry for the last 20 years.

Pendulums, springs, and natural frequencies

Posted by Ankit On May 21st, 2011

I remember while preparing for the JEE I came across a simple spring mass system and was quite surprised by the fact that it should have a natural frequency at which it must vibrate when left to its own devices. An analogous but more intuitive system is a regular clock pendulum. The pendulum completes one cycle in exactly a second, and, therefore, has a natural frequency of 1 Hz. It used to fascinate me that the pendulum should do just that without any external intervention (There is some external intervention to make up for energy dissipations from air viscosity, friction etc. but we'll neglect those 'non-ideal' effects for now.)

So Â I was thinking about the simple spring mass system the other day and was quite pleased with the fact that one can explain the 'complicated concept' of natural frequencies in terms of purely physical intuition. Think of a spring which is attached to a wall at one end and a block which is free to move back and forth at the other end. The spring is made up of a material whose weight is much smaller than the weight of the block (assumption of massless spring) and the whole assembly is placed on a very slippery surface (assumption of frictionless surface.) Let's call the initial location of the block which corresponds to zero stretching in the spring, Â 'S'. Now we take the block and pull it so that the spring stretches by say 5 cm. and leave it. If one has ever held a spring in hand he knows that it takes effort to stretch it. In fact, it becomes progressively more difficult to stretch the spring to larger lengths. The same it true with compressing it - so the spring has a tendency to force itself to an unstretched position. Therefore, in our spring block system, the spring pulls the block back and keeps pulling it till the spring reaches its unstretched position. But by this time the block has attained a velocity so it doesn't stop and starts compressing the spring. The spring tries to stop this compression but it takes a certain amount of time before the spring is able to bring the block to a stop. By that time the block has already compressed the spring by a certain distance and that distance is exactly equal to the initial stretching of the spring (5 cm. in this case.) So our initial stretch has been completely converted into an equivalent compression. Now that the block is at rest again, the spring starts pulling it back until it crosses 'S', starts stretching the spring due to its speed, and stops when the spring is stretched by 5 cm. This whole cycle of stretching-compression-stretching takes a certain amount of time and now we ask ourselves a question, is it possible for this time to be any less than what it is? We also put the constraint, for the time being, that the amplitude of vibration (5 cm. in this case) has to be the same. For that to be the case, the block would have to travel at a higher speed on average and stop faster. This also means that it will have to be traveling at a higher speed when it crosses 'S'. But if that is the case, the spring will not be able to stop it within 5 cm. If the spring wants to stop it within 5 cm., it will have to be a stiffer spring but that is not allowed in our current thought experiment. Now let's relax the constraint that the amplitude of vibration has to be 5 cm. But that is again problematic because now the block has to travel a larger distance to complete one cycle. So even though it may be traveling at a higher speed on average, it will still take the same amount of time due to the larger distance it has to cover in each cycle.

This brings us to the conclusion that as long as we do not change the spring and the mass, we cannot change the time the system takes to complete one cycle - and this precisely is the natural frequency of the system - a constant for this simple system! In fact, as argued above, it is possible to complete the cycle in a faster time (higher frequency) if the spring is stiffer. It's even possible to do it with the same spring if we decrease the weight of the block - because it's easier to stop lighter objects than heavier objects. So the frequency of our system (number of cycles in a second) seems to increase with increasing stiffness and decreasing mass. Well, that's about how much we can deduce without mathematics! The exact relation is frequency=C*{k/m}^.5, where 'k' is the stiffness of the spring and 'm' is the mass of the block (C is a constant.)

The pendulum is a very analogous system where the effect of the spring is replaced by the pull of gravity. In fact, a lot of systems in the real world are walking this tightrope where there exists a certain force which wants to pull them back to a rest position. In a more complicated way, they all display preferences for certain 'frequencies'. They all want to complete their cycles in a certain time. It's all very drab and academic when a spring-mass system does that but it's all so artistic and cultured when a violin does the exact same thing!

Recursion

Posted by Ankit On April 4th, 2011

Today I was thinking about recursion and came across this famous painting by Escher,

Rain

Posted by Ankit On March 20th, 2011

I'm sitting here, near my window, and the heavy sky is throbbing above in deep grunting discolored voices, threatening the pane with ominous liquid possibilities. I quite like the word liquid. It's terse, handsome and upright. If I were to bestow upon it the vestiges of a human form, I would imagine it to be a man sharply dressed in a black tuxedo, reserved, graceful, and erudite, but one who has hidden beneath his charming facade a life, a disposition, a history quite sinister. Now I can hear the noise of rain outside. A river of sounds in which the individual drops have sacrificed their identities and produced after an eternity of fall a moment of both aural and visual poignancy - a perfect pear, tranquil and transparent, upon whose surface the Sun had poured the fruits of his deliberations, disintegrating into its formless constituent after touching the philistine contours of my window. I also notice that the vague impression of rain which I receive filtered through the window is probably more beautiful, more evocative than the actual rain itself - as if its essence, the rainness of rain, has been distilled through the clear glass and I receive not the knowledge of this particular instance of precipitation but a deeper more abstract experience which stands proxy to all those junctions of my life which were made slower and more beautiful by the cold, wet, and cozy presence of rain. The weather is brisk, the air quietened by the steady beat of falling drops - a low constant note, a canvas which has been uniformly painted in a dark hue, the background taste of salt, the default response to the questions of a questionnaire - an abstraction which is chipping away reality at its edges and inducing in me the fantastic images which are the harbinger of deep sleep.

Abhiman

Posted by Ankit On February 21st, 2011

In this vast sea of human interactions, upon whose surface emotions, both tragic and comic, poignant and trivial, ebb and flow, gather momentum and break, and mix in a turbulent confusion, every so often there comes along a little line, a piece of poetry, a thought at once both supremely elegant and precisely striking, even to the point of being heartbreaking, and it extracts from the chaos of reality in which love melts into hatred and the boundaries of emotion and intention are vague, a unification, an understanding, a concept which shines clear like a bush backgrounded by mist, an idea which hangs delicately in space, constant, unswerving, like a hesitant melodious violin whose sounds seems to be coming from afar, crisp within the tumult of the violas and the piano.

In the movie Raincoat, Shubha Mudgal pines 'Piya tora kaisa abhiman (My lover, why do have this pride),' and it's one of those beautiful moments when a part of this arbitrary reality has been shocked into submissiveness and it presents itself melted along the beautiful contours of the artist's sensitivity. Just a few words, and one feels the infinite desperation of the lover with a poignancy which would only have been reduced, had an effort been made to explain it away. She sits there waiting for him and he doesn't arrive. And as time slips through her fingers like heartless grains of sand, she can only wonder, in mute resignation, what pride prevents him from coming to her. His actions are incomprehensible to her and yet, as the lines almost give away, she is trying hard to understand and would do all that is within her means and more, if only he came back and talked with her. But he doesn't come and she can only wonder...

This reminds me of another beautiful line from Ghulam Ali's 'Chupke Chupe raat din which goes,

Berukhi ke saath sun-na darde dil ki daastan

Wo kalaai mein tera kangan ghumana yaad hai

(I remember how you were fiddling with your bangles, when I was trying to tell you the story of my heartbreak)

The fourth wall

Posted by Ankit On February 7th, 2011

I know this will be irrelevant soon. And it'll be lost if you're seeing this in the feed.

A little stopmotion

Posted by Ankit On January 9th, 2011

I was watching Coraline the other day and decided to do a bit of stopmotion animation myself. This is where you take a lot of photos, moving things little by little, and after a hell lot of time and a severe backache, run them quickly one after each other and watch your 3 hours getting condensed to 40 seconds. So here is my table cleaning itself (original photos taken with my phone):

I wanted to add some sound and some text but my propensity for slack seems to have gotten the better of myself at this point.

Genealogy

Posted by Ankit On November 25th, 2010

I have been wanting to trace my family history for a long long time now. The reason for this is as follows: I am perfectly aware that there is no such thing as the golden age of humanity, and neither was there ever an innocent generation devoid of all malice and hardship. Human struggle and trepidation is one uniting factor which bridges people across decades and centuries. Looking back through the glasses of nostalgia we run the risk of painting a very untrue picture of the past. A picture where people were more honest, families were stronger and nobler, individuals were wiser - a picture which is untrue because it ignores the fact that humans have always been and will always be just that, merely human. They will be dissatisfied as they have been through the centuries. They will have struggles as they have always had. The form of these struggles change but the essence remains intact. I get a rush when I can give relatable names to these individuals who lived hundreds of years ago, who probably lived a very ordinary, very uphill, and very human life but who hold a special position in my life by virtue of being my ancestors. I can then move up my chain and witness generations after generations of names I have heard occupying their own little 60 years of sunshine withering away against the onslaught of time. Their legacy is merely the gift of the next generation - only to vanish in another 60 years. And every single one of those hundreds upon thousands of individuals probably thought their child was the chosen one and that they themselves had a special understanding of life. Every single one of them probably had staunch religious, casteist, and national loyalties, a whole edifice of moral beliefs, a little house where they started a family, an income avenue, people they disliked, individuals they loved, stupid, unflinching ideas, ideas they were probably right about and ideas they were completely wrong and shortsighted at, a whole system of cuisine, a language which was perhaps very different from what I speak now. Some of them might have stood in the courts of nawabs or princes, most of them probably had dark lingering secrets, all of them contributed to this vast pulsating sea of drama which is life and upon whose surface ebb and flow the waves of human emotions. It's simply fascinating.

So I finally made a site, Genealogy, through which I hope I will be able to trace my family's ancestry through time and space. While I am stuck here in India at the whims and fancies of the US department of state, I am trying to make use of this time by gleaning as much information as I can. In so doing I came across the diary of my maternal grandfather. Now he was a special person, the kind of person which, I am afraid, doesn't exist in my family anymore and is very rare to come across even outside of the family. My memories of him consist of him sitting me by his side in a cozily lit room on a cold December evening at my uncle's Dairy colony house in Gorakhpur and telling me stories from sources as varied as Mahabharata and Tolstoy. His formal education consisted merely of matriculation (it might have been a lot in 1940s) and all his life was spent in the Railways but that did not prevent him from harboring an immense respect for knowledge. It seemed to me that he managed to do something which only occurs sparingly: he managed to save the primal curiosity which everyone is blessed with from the eroding winds of life. And I see it in his diary. Little episodic entries, quite disconnected, completely useless to a man of the world, but how I love them for their utter futility. I think I understand how happy and fascinated he must have felt when he learned that our star is one in a hundred billion stars in the Milky Way, how satisfied it must have made him to list down the Aaroh and Avroh of Darbari, how happy he must have become while roaming alone on the streets of old Lucknow amidst the Nawabi ruins and the cultural landscape. There is no pretense, no malice, and no regret, just a childlike curiosity and a desire to know more. How I wish I could talk to him now so that I could ask him the one question I want to ask all the old people, 'How has it been?', and get a special answer.

Haircut et. al.

Posted by Ankit On October 23rd, 2010

Haircut is one of those things which never seems to have been done well. It's like a photograph which inadvertently makes you wonder what the reason was for your dumb expression. You always feel that something in the photo is not quite right and things could have been a whole lot better if only you had tilted your head slightly to the right or restrained that retarded smile by a smidgen. You subconsciously blame the harsh light, the heartless, uncultured flash, the amateur framing, the colors of your clothes which seem to stand out like a sore thumb, and the rest of the humanity in general which has made your day a little less enjoyable just by existing inÂ a way which falls short of your exacting measures. You fidget, you shuffle, you empty out your pockets and scrape the bottom of the barrel looking for excuses as to why, oh why, the photo doesn't look quite right. And amongst all this deliberation the elephant in the room is just you, with your features which were never really selected by nature by the yardstick of how well they frame within a 4 by 6. Even if your features do not look as if they have been picked straight out from an Evil Dead sequence, the humbled 'creation' has never really been so good so as to make a specimen which is satisfied in its own eyes.

I mentioned all this because I wanted to connect it to the dilemma of the bad haircut. While sitting in the barber's chair with him snipping away at my locks with the nonchalance of a 'mere job', I often wonder which exactly is the point where he botches it all up. Because it seems to me that I have never really had a good haircut (Burrito Barber excluded out of kinship.) Not only have I not had a good haircut, I always have a feeling that while I am sitting there in that 'execution chair', my throat restrained by piece of cloth which never seems to perform its purpose of preventing hair from sneaking under my shirt, the guy with the scissors doesn't know what he is doing. It's a huge charade all over the place really. I sit there pretending that I feel that he knows what he is doing. He senses that I am not being honest but he has a reputation to protect and a bread to win and goes on pretending that he knows what he is doing. And bound in this little knot of mutual suspicion, the two of us embark on a journey which has a vague beginning, an unsure progression, and a muted, disastrous end. I pay up not because he did a good job but because he didn't break the charade and made it uncomfortable all over the place. I think we both understand that we are related. We are both related by ineptitude and cowardice. We understand that we are both puppets in a show where society expects hair to be trimmed periodically. Nature has played a vile trick in Keratine which likes to grow and society has decided that it's unacceptable. And the barber and I are hopelessly stuck in this battle of titans.

But maybe I am just making excuses. Maybe, like the photograph, I was never meant to have a good haircut. Some people can never become mathematicians, some can never balance things on their heads, some people can never have a good haircut. I remember when I was young my mother had me part my hair from the side. I never really liked it, having associated it with the kind of boys who sit on the first bench and raise their hands to answer questions - the kind I hate to this day. So when my turn came for rebellion, as it comes for everyone, I rebelled by shifting the location of my parting a few inches to the right. That was pretty much the most violent gesture I can ever be accused of committing. But the flip side of this transgression, as I have come to suspect, is eternal damnation. I have come to believe that my hair was meant to be parted from the side and nature never really intended it to have a center parting. Therefore, whenever I go to a barber with my very affected center parting, he looks at me with a confused stare, goes around trying to figure out what's there with my hair which is not quite right, gives up, becomes self conscious, pretends that he knows what he is doing, induces an uncomfortable silence, and begins snipping away. If only I could give him the historical account of side parting, maybe he'll do a better job.

But I say that I have never had a good haircut with a few qualifications. One is obviously burrito barber but that is more because I have not yet bought the promised burrito, and the other is the barber I had today. This girl was what Van Gogh would have been had he decided to cut hair. I am not saying that I had a good hair cut. I am just saying that I was completely mesmerized by her craft. She didn't care a damn how to suit my hair to my needs. I entered the saloon, she pursed her lips and squinted her eyes as if she did not at all approve of my existence, inquired if I had been living in a cave, decided that my hair was too long - objectively too long - and after 10 minutes of pure 'barbaric' mastery, said that this was just better - objectively better. And through the process I could only be completely enthralled by here sure scissor, her deft hand movements, her elegant, measured, actions. I think I am not conveying my total amazement properly. And I cannot because it's impossible to convey how one truly feels at reading Nabokov, or listening to Beethoven, or watching Federer play. It's impossible to convey how much of a pleasure it was to be sitting there watching her convert a vague lump of clay to a vase she thought was at least presentable. Oh what a joy!